Hamming Code

A Hamming Code is a version of forward error correction involving introducing redundancy bits through out the data in order to be able to reconstruct missing bits, in a similar process to a parity check.

Encoding

A given piece of data can be encoded into it’s Hamming Code representing by:

1. Calculating The Size

To make this efficient, we want to know the size of the output data in advance so we can heap allocate it. Hence, we need to first calculate the number of redundancy bits we need, which is given by the formula:

Formula

$k=2^r-r-1$

Where:

• $k$ is the new message length
• $r$ is the length of the input data

We can then solve for the size by adding this new result to the existing string size.

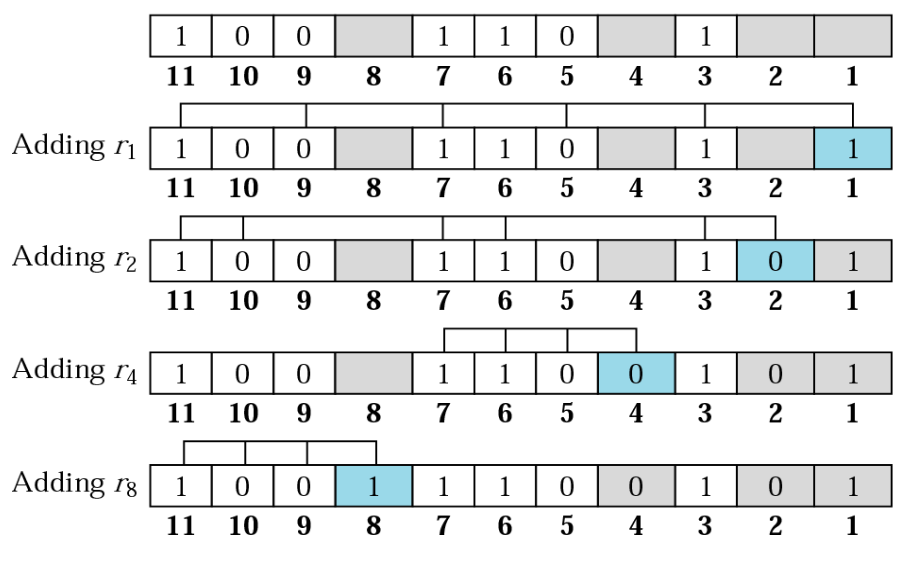
2. Interspersing Redundancy Bits

Next, we allocate a new piece of data where we intersperse a series of parity bits (after deciding if it should be even or odd) at every $2^n$ positions.

Note

The presence of multiple redundancy bits allows to check for burst errors and single-bit errors.

Using powers of two specifically allows us to pinpoint the exact bit where single bit errors occur.

The coverage for each parity bit looks something like:

Label	Bit	Bit	Bit	Bit	Bit	Bit	Bit
Position (Decimal)	$7$	$6$	$5$	$4$	$3$	$2$	$1$
Position (Binary)	$111$	$110$	$101$	$100$	$011$	$010$	$001$
Type	data	data	data	parity	data	parity	parity
Coverage (P1)	X		X		X		X
Coverage (P2)	X	X			X	X
Coverage (P3)	X	X	X	X

This coverage pattern makes it so that every single bit has it’s own unique pattern of failing parity checks, making it easy to identify.